Algorithm
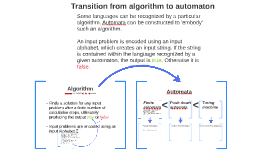
Transcript: _ Σ0={ε} the empty string Σ = Σ1 = {a,b} all strings (|x|=1) of length 1 _ Automata ex. Σ = {a,b} A = {aa, ab, ba} A={w|w contains a and |w|=2} A = {ε, a, b, bb, aaa...} A={w|w !(contains a) or |w|!=2} (Languages containing only 1 element are called Singleton languages) ex. Σ = {a,b} A = {aa, ab, ba} A={w|w contains a, |w|=2} B = {ab, ba, bb} A={w|w contains b, |w|=2} AUB = {aa, ab, ba, bb} AUB={w|w contains a or b, |w|=2} Context free languages (2 elements, in the case of this alphabet) Muhammed AL CHWARIZMI - 8th - 9th century A U B = {x < Σ* | x < A v x < B} REG = {L(M) | M is a DFA} The length of the input string determines the number of calculation steps So each symbol of the input string represents a calculation step The output is given after the last symbol has been processed A PDA Some languages can be recognized by a particular algorithm. Automata can be constructed to 'embody' such an algorithm. An input problem is encoded using an input alphabet, which creates an input string. If the string is contained within the language recognized by a given automaton, the output is true. Otherwise it is false. (0 elements) ={} the empty set DFA ( <{ε}<Σ*) ex. Σ = {a,b} A = {aa, ab, ba} A={w|w contains a, |w|=2} B = {ab, ba, bb} A={w|w contains b, |w|=2} A o B = {aaab, aaba, aabb, abab, abba, abbb, baab, baba, babb} A o B={w1w2|w1 contains a, |w1|=2, w1 contains b, |w2|=2} |A o B| = |A| x |B| A o B = AB (=aB when A={a}=singleton language) AAA=A3=An, n=3 A* = An(n>=0) A+= An(n>0) = AA* Push down automata A U B DPDA NFA A = {x < Σ* | x !< A} A ∩ B = {x < Σ* | x < A, x < B} Z = {q0, q1, q2,..., qn} a set of states Σ = {a, b} an input alphabet δ : Z x Σ --> S a transition function q0 = the start state E = {q1, q2} a set of final states < Turing machine An alphabet Σ = {a1, . . . , am} is an ordered set consisting of a limited number of symbols (represented here by "a") A sequence x = x1 . . . xn where each "x" represents a symbol from the input alphabet, is an input string Σn = all strings of length n Σ* = all strings of every length, including Σ0 = the only word of length 0: ε = the empty string Every subset L < Σ* is a language derived from Σ _ A ∩ B Algorithm The langue recognized by M is L(M), where M finds itself in a final state after processing the last symbol of the input string Regular languages A o B < Finds a solution for any input problem after a finite number of calculation steps, ultimately producing the output true or false Input problems are encoded using an input Alphabet Σ _ A Deterministic Finite Automaton (M) is composed of 5 parts: Transition from algorithm to automaton Context sensitive languages Language operations Σ*={ε,a,b,aa,ab,ba,bb,aaa...} Finite automata ex. Σ = {a,b} A = {aa, ab, ba} A={w|w contains a, |w|=2} B = {ab, ba, bb} A={w|w containts b, |w|=2} A∩B = {ab, ba} A∩B={w|w contains a and b, |w|=2} A o B = {xy | x < A, y < B} Σ ={a,b}